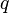 . Esta constante
. Esta constante 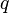 é chamada razão da progressão geométrica. A letra q foi escolhida por ser inicial da palavra quociente.
é chamada razão da progressão geométrica. A letra q foi escolhida por ser inicial da palavra quociente.Alguns exemplos de progressão geométrica:
 , onde
, onde 
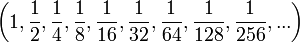 , onde
, onde 
 , em que
, em que 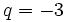
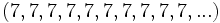 , em que
, em que 
 , em que
, em que 
Soma dos termos de uma P.G.
A soma dos termos de uma P.G., a partir do primeiro, é definida por: , veja notação de somatório
, veja notação de somatório
Demonstração
Essa fórmula pode ser explicada assim. Escreva: e o resultado segue.
e o resultado segue.Soma dos infinitos termos de uma P.G.
A soma dos infinitos termos de uma P.G. é chamada série geométrica e está bem definida quando | q | < 1. Sua soma é: e a1 > 0 então sua soma é mais infinito e se
e a1 > 0 então sua soma é mais infinito e se  e a1 < 0, sua soma é menos infinito.
e a1 < 0, sua soma é menos infinito. , por exemplo. Observe também que q pode ser complexo. O tratamento destas séries pode ser visto no artigo sobre séries divergentes.
, por exemplo. Observe também que q pode ser complexo. O tratamento destas séries pode ser visto no artigo sobre séries divergentes.Produto dos termos de uma P.G.
O produto dos termos de uma Progressão Geométrica, a partir do primeiro, é dada por: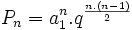
O produto também pode ser determinado sem o conhecimento da razão:
 , sendo similar à forma do Somatória da P.A.
, sendo similar à forma do Somatória da P.A.Classificação das progressões geométricas
As P.G. podem ser classificadas em cinco grupos conforme o valor de q.Progressão geométrica constante.
Uma progressão geométrica constante é toda progressão geométrica em que todos os termos são iguais, sendo que para isso a razão q tem que, caso a1 diferente de 0(zero), ser sempre 1 ou 0 (nulo).
Exemplos de progressão geométrica constante:
- P.g.(1,1,1,1,1,1,1,1,1,...) - razão q = 1
- P.g.(0,0,0,0,0,0,0,0,0,...) - razão nula ou indeterminada
Progressão geométrica crescente
Uma progressão geométrica crescente é toda progressão geométrica em que cada termo, a partir do segundo, é maior que o termo que o antecede, sendo que para isso há dois casos: para a1 positivo a razão q tem que ser sempre positiva e maior que 1 e para a1 negativo a razão q tem que ser positiva e menor que 1.Exemplos de progressão geométrica crescente:
- P.G. (1,2,4,8,16,32,64,128,256,512,1024,2048,4096,...) - razão q = 2
- P.G. (2,6,18,54,162,486,1458,4374,13122,...) - razão q = 3
- P.G. (-100,-10,-1,-0.1,-0.01,-0.001,-0.0001,-0.00001,...) - razão q = 1/10
Progressão geométrica decrescente
Uma progressão geométrica decrescente é toda progressão geométrica em que cada termo, a partir do segundo, é menor que o termo que o antecede, sendo que para isso há dois casos: para a1 positivo a razão q tem que ser sempre positiva e menor que 1 e para a1 negativa a razão q tem que ser positiva e maior que 1.Exemplos de progressão geométrica decrescente:
- P.G. (-1,-2,-4,-8,-16,-32,-64,-128,-256,-512,-1024,-2048,-4096,...) - razão q = 2
- P.G. (8,4,2,1,1/2,1/4,1/8,1/16,1/32,1/64,1/128,...) - razão q = 1/2
Progressão geométrica oscilante
Uma progressão geométrica oscilante (ou alternante) é toda progressão geométrica em que todos os termos são diferentes de zero e dois termos consecutivos tem sempre sinais opostos, sendo que para isso a razão q tem que ser sempre negativa e diferente de zero.Exemplos de progressão geométrica oscilante:
- P.G. (3,-6,12,-24,48,-96,192,-384,768,...) - razão q = -2
- P.G. (1,-1,1,-1,1,-1,1,-1,1,-1,1,-1,...) - razão q = -1
Progressão geométrica quase nula
Uma progressão geométrica quase nula é toda progressão geométrica em que o primeiro termo é diferente de zero e todos os demais são iguais a zero, sendo que para isso a razão q tem que ser sempre igual a zero.Exemplos de progressão geométrica quase nula:
- P.G. (8,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,...) - razão q = 0
- P.G. (-169,0,0,0,0,0,0,0,0,0,0,0,0,0,0,0,...) - razão q = 0
- Progressão Aritmética Geométrica
O interessante, neste caso, é obter uma fórmula geral para a soma de n termos.
Definição por recursão e fórmula do termo geral
Costuma-se denotar por an n-ésimo termo de uma progressão geométrica. Assim, a progressão fica totalmente definida pelo valor de seu termo inicial a1 e sua razão q.A sucessão dos termos é obtida por recursão:
linguagem de programação C), pode ser conveniente considerar que o termo inicial da PG tem índice zero (a0). Neste caso, o termo geral fica:



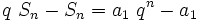
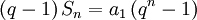







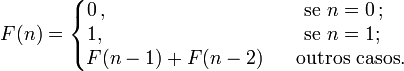

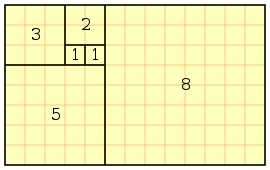

 . O número
. O número  , em que r=3(por que o numero do r é a diferença entre os números que vão crescendo)\,\!.
, em que r=3(por que o numero do r é a diferença entre os números que vão crescendo)\,\!. , em que
, em que  .
.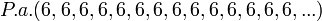 , onde
, onde 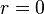 .
.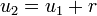
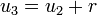



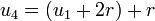

 Outra fórmula útil expressa o n-étimo termo em função do m-étimo termo:
Outra fórmula útil expressa o n-étimo termo em função do m-étimo termo: 

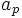 e
e 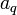 é:
é: